Surface Free Energy | Measurement of Surface Tension - Important Questions

Physical Pharmacy Important Questions on Surface Free Energy & Measurement of Surface Tension - Interfacial phenomena

Important Questions:

1. Define Surface Free Energy.
2. Derive an equation for determination of Surface Free Energy. ΔG = γΔA OR  W = γ x ΔA.
3. Write applications of surface free energy equation in pharmacy?
4. Deduce an equation to derive pressure difference across curved surface. ΔP = 2γ/r.
5. Write application of concept of pressure difference across curved surface.
6. Explain capillary size method for determination of surface tension of liquid. Derive equation of capillary rise method with neat and clean diagram. γ = rhρg/2
7. Give 3 instances of capillary rise in nature.

For Derivation by capillary rise method..

Step I: Calculate force due to upward component.

Step II: Calculate force due to downward component.

Step III: Equate both opposing forces. Upward component = downward component. 2πrγ = πr²hρg. γ = rhρg/2.

Important Questions with Solution:

1. Define Surface Free Energy.

    Surface tension maintains the surface area of a liquid to a minimunm value. The surface area can be increased provided some work is being done against the force at the surface.

    Surface free energy is defined as the work required to increase the area of a liquid by 1 sq cm.

    As per the definition, the surface free energy is equal to the surface tension.

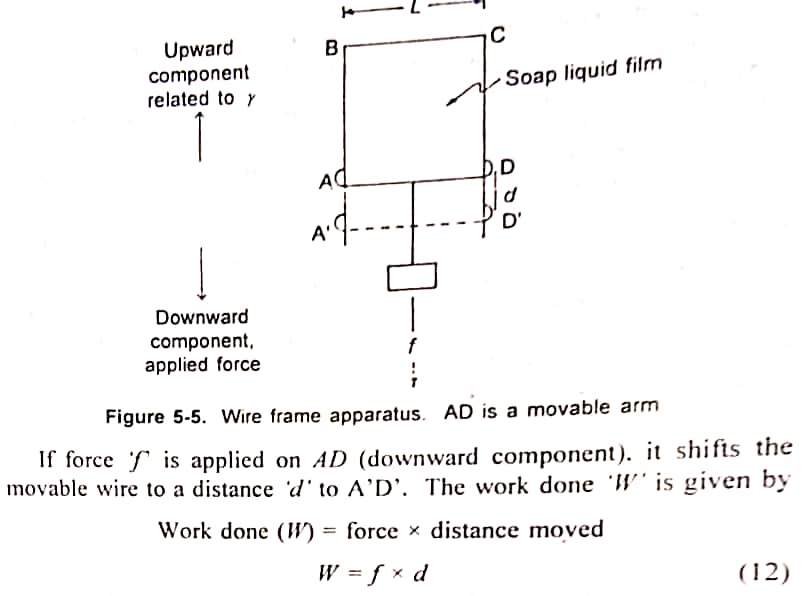
2. Derive an equation for determination of Surface Free Energy. ΔG = γΔA OR  W = γ x ΔA.

    Derivation for determination of Surface Free Energy is as follows:

    ABCD is a rectangular wire as shown in figure below. The side of AD = L and is movable. A drop of soap solution is placed on the frame, so that it forms a film within the frame. The side AD remains stable on account of surface tension exerted by the soap film. When force (such as hanging mass) is applied downward, the film gets stretched a the movable bar AD goes down until the film breaks.

    When the applied force is less than that is required for breaking, the film would retract on account of surface tension.

    in which 'W' is the Work done or surface free-energy increase (ΔG) cxpressed in ergs. In a thermodynamics sense, any form of energy can be divided into an intersity factor and a capacity factor. In this case, surface tension is the intersity factor and a capacity in area is the capacity factor.

3. Write applications of surface free energy equation in pharmacy?

     The surface free energy equations is applied in a number of fields in pharmacy as follow:

1. adsorption gases on the solid surface.
2. physical instability of suspensions.
3. thermodynamic instability of emulsions

4. Deduce an equation to derive pressure difference across curved surface. ΔP = 2γ/r.

    When a glass tube is placed in water, lower miniscus (curved surface) is normally observed at the surface. This effect is due to surface tension. Hence, surface tension can be explained is terms of the pressure difference across the curved interface. Globules in an emulsion represent curved surfaces. Such surfaces are also observed in aerosols.

Change in surface free energy = -8πγrdr

The minus sign indicates the shrinkage of the bubble.

   The opposing force: This energy is the pressure difference, 'ΔP' across the film. Since the pressure is force can be written as:

5. Write application of concept of pressure difference across curved surface.

6. Explain capillary size method for determination of surface tension of liquid. Derive equation of capillary rise method with neat and clean diagram. γ = rhρg/2

7.Give three instances of capillary rise in nature.

    Phenomenon of capillary rise is observed in several instances in nature. A few familar examples are:

1. Underground water rising on to the surface.
2. Oil rising through wick in a lamp.
3. To certain extent, water rising from soil to the branches above the ground in plants.